Fórmula de tiempo, velocidad y distancia: 4° grado. ¿Cómo encontrar el tiempo, sabiendo la velocidad y la distancia? ¿Cómo encontrar la velocidad si se conocen el tiempo y la distancia? ¿Cómo encontrar la distancia si se conocen el tiempo y la velocidad? Gráfica de la dependencia de la velocidad del cuerpo con el tiempo

¿Cómo resolver problemas de movimiento? La fórmula para la relación entre la velocidad, el tiempo y la distancia. Tareas y soluciones.

La fórmula para la dependencia del tiempo, la velocidad y la distancia para el 4º grado: ¿cómo se indican la velocidad, el tiempo y la distancia?

Las personas, los animales o las máquinas pueden moverse a cierta velocidad. Pueden ir de cierta manera en un tiempo determinado. Por ejemplo: hoy puedes llegar a tu escuela en media hora. Caminas a cierta velocidad y recorres 1000 metros en 30 minutos. En matemáticas, el camino que se supera se denota con la letraS. La velocidad se denota con la letra v. Y el tiempo durante el cual se recorre el camino se denota con la letra t.

• Ruta —S
• Velocidad — v
• Hora —t

Si llega tarde a la escuela, usted el mismo puede recorrer el camino en 20 minutos, aumentando su velocidad. Esto significa que el mismo camino se puede recorrer en diferentes tiempos y a diferentes velocidades.

¿Cómo depende el tiempo de viaje de la velocidad?

Cuanto más rápida sea la velocidad, más rápido se cubrirá la distancia. Y cuanto menor sea la velocidad, más tiempo se tardará en completar el viaje.

​​

¿Cómo encontrar el tiempo sabiendo la velocidad y la distancia?

Para encontrar el tiempo que tomó recorrer una distancia, necesitas saber la distancia y la velocidad. Si divides la distancia por la velocidad, sabrás el tiempo. Un ejemplo de tal tarea:

La tarea sobre la liebre. La Liebre se escapó del Lobo a una velocidad de 1 kilómetro por minuto. Corrió 3 kilómetros hasta su hoyo. ¿Después de algún tiempo Hare corrió hacia el agujero?

¿Qué tan fácil es resolver problemas de movimiento en los que necesita encontrar la distancia, el tiempo o la velocidad?

1. Lea el problema cuidadosamente y determine qué se sabe de la condición del problema.
2. Escriba estos datos en el borrador.
3. Escribe también lo que se desconoce y lo que se encuentra
4. Usa la fórmula para problemas de distancia, tiempo y velocidad
5. Introduce el datos conocidos en fórmula y resolver el problema

Solución para el problema de la liebre y el lobo.

• De la condición del problema, determinamos que conocemos la velocidad y la distancia.
• También determinamos a partir de la condición del problema que necesitamos encontrar el tiempo que tardó la liebre en correr hasta el hoyo.

Escribimos estos datos en un borrador por ejemplo:

Distancia al hoyo — 3 kilómetros

Velocidad de la Liebre — 1 kilómetro en 1 minuto

Se desconoce el tiempo

Ahora escribamos lo mismo en símbolos matemáticos:

S— 3 kilómetros

V — 1 km/min

t—?

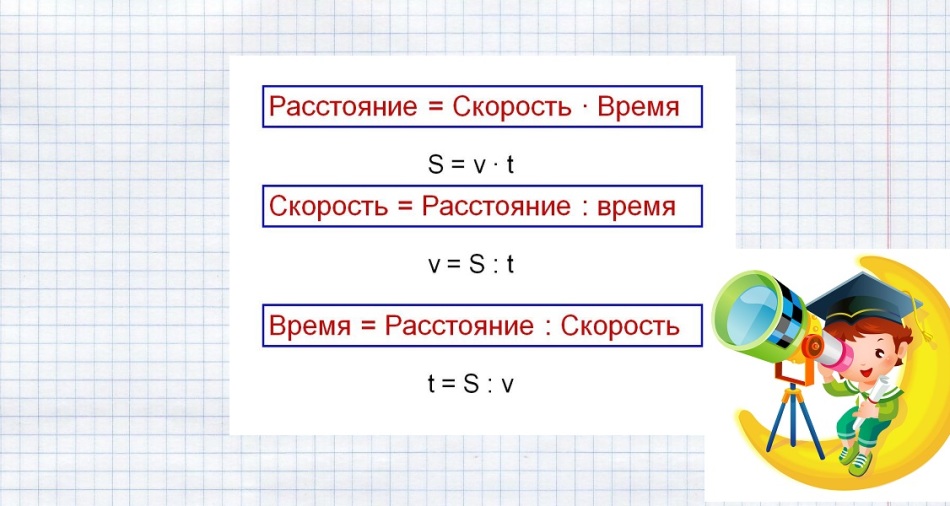
Recordamos y anotamos la fórmula para hallar el tiempo en un cuaderno:

t = S: v

Ahora escribimos la solución del problema en números:

t = 3: 1 = 3 minutos

¿Cómo encontrar la velocidad si se conocen el tiempo y la distancia?

Para encontrar la velocidad, si se conocen el tiempo y la distancia, la distancia debe dividirse por el tiempo. Un ejemplo de tal tarea:

La liebre se escapó del lobo y corrió 3 kilómetros hasta su agujero. Cubrió esta distancia en 3 minutos. ¿Qué tan rápido corrió la liebre?

La solución al problema del movimiento:

1. En el borrador escribimos que conocemos la distancia y el tiempo.
2. A partir de la condición del problema, determinamos que necesitamos encontrar la velocidad
3. Recordamos la fórmula para encontrar la velocidad.

Las fórmulas para resolver tales problemas se muestran en la siguiente imagen.

Sustituye los datos conocidos y resuelve el problema:

La distancia al hoyo es de 3 kilómetros

El tiempo que tardó la Liebre en llegar al hoyo fue de 3 minutos

La velocidad es desconocida

Escribamos estos datos conocidos en símbolos matemáticos

S— 3 kilómetros

 t— 3 minutos

v —?

Escribimos la fórmula para encontrar la velocidad

v = S: t

Ahora escribimos la solución del problema en números:

v = 3: 3 = 1 km/min

Cómo encontrar la distancia si el tiempo y la velocidad se conocen?

Para encontrar la distancia, si se conocen el tiempo y la velocidad, multiplique por la velocidad. Un ejemplo de tal tarea:

La Liebre se escapó del Lobo a una velocidad de 1 kilómetro en 1 minuto. Le tomó tres minutos correr hasta el hoyo. ¿Qué distancia corrió la liebre?

Solución del problema: Escribimos en el borrador lo que sabemos de la condición del problema:

La velocidad de la Liebre es de 1 kilómetro en 1 minuto

Tiempo que corrió la liebre hasta el hoyo - 3 minutos

Distancia - desconocida

Ahora, escribamos lo mismo en símbolos matemáticos:

v — 1 km/min

t— 3 minutos

S —?

Recordamos la fórmula para encontrar la distancia:

S = v ⋅ t

Ahora escribimos la solución del problema en números:

S = 3 ⋅ 1 = 3 km

¿Cómo aprender a resolver tareas más complejas?

Para aprender a resolver tareas más complejas, debe comprender cómo resolver tareas simples, recuerde qué signos indican distancia, velocidad y tiempo. Si no puede recordar fórmulas matemáticas, debe escribirlas en una hoja de papel y tenerlas siempre a mano cuando resuelva problemas. Resuelva tareas sencillas con su hijo que se le ocurran sobre la marcha, por ejemplo, durante un paseo.

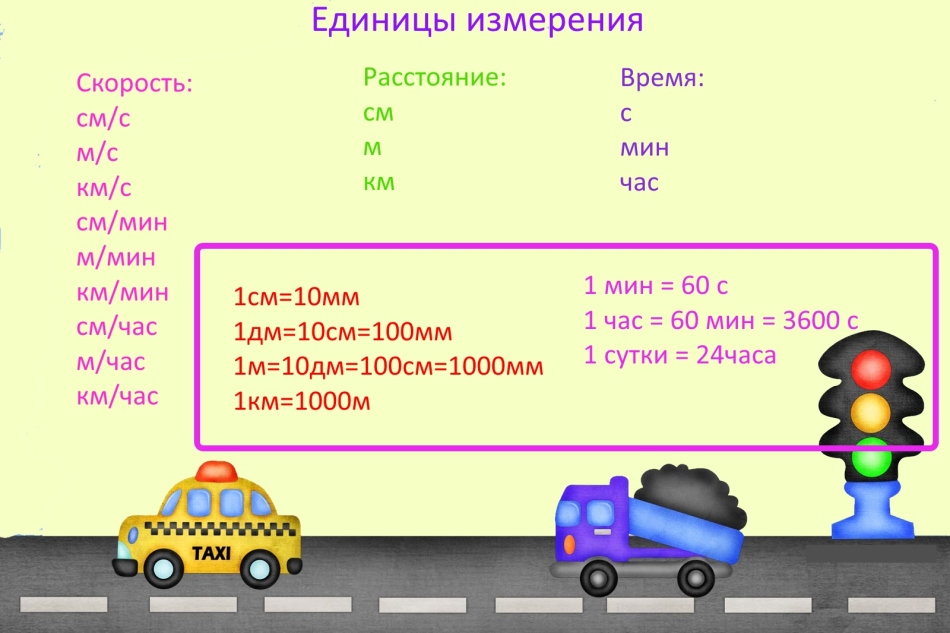
Unidades de medida

Al resolver problemas de velocidad, tiempo y distancia, muchas veces se equivocan porque olvidan convertir las unidades de medida.

IMPORTANTE: Las unidades de medida pueden ser cualquiera, pero si hay diferentes unidades de medida en el mismo problema, conviértalas a la misma. Por ejemplo, si la velocidad se mide en kilómetros por minuto, entonces la distancia debe representarse en kilómetros y el tiempo en minutos.

Para curiosos : El sistema de medidas generalmente aceptado se llama métrico, pero no siempre fue así, y en la antigua Rusia se usaban otras unidades de medida.

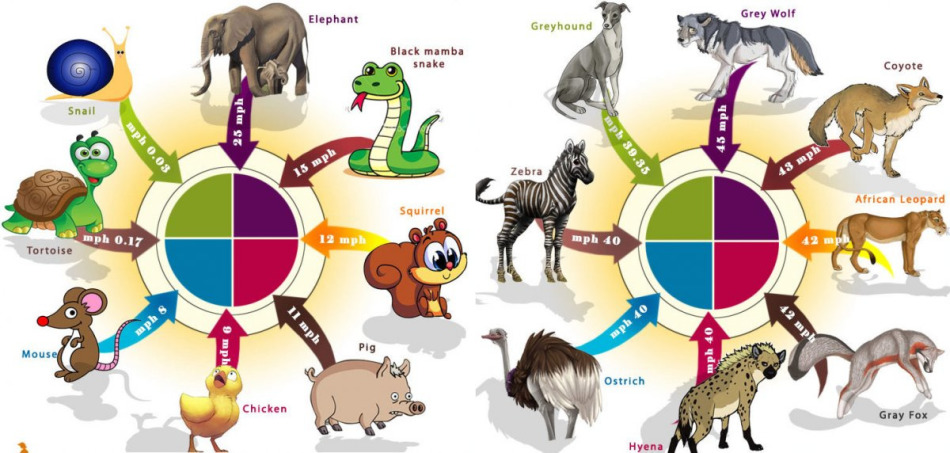
Problema de la boa : El bebé elefante y el mono midieron la longitud del boa en pasos. Se movieron uno hacia el otro. La velocidad del mono fue de 60 cm en un segundo y la velocidad del elefante bebé fue de 20 cm en un segundo. Pasaron 5 segundos en la medición. ¿Cuál es la longitud de la boa? (solución debajo de la imagen)

<> Solución:

A partir de la condición del problema, determinamos que conocemos la velocidad del mono y del elefante bebé y el tiempo que necesitaron para medir la longitud de la boa.

Anotemos estos datos:

La velocidad del mono es de 60 cm/seg

La velocidad del elefante bebé es de 20 cm/seg

Tiempo — 5 segundos

Distancia desconocida

Escribamos estos datos en símbolos matemáticos:

v1 — 60 cm/seg

v2 — 20 cm/seg

t — 5 segundos

S —?

Escribamos la fórmula de la distancia, si se conocen la velocidad y el tiempo:

S = v ⋅ t

Contemos la distancia que recorrió el mono:

S1 = 60 ⋅ 5 = 300 cm

Ahora vamos a contar cuánto ha caminado el bebé elefante:

S2 = 20 ⋅ 5 = 100 cm

Sumamos la distancia recorrida por el mono y la distancia recorrida por el bebé elefante:

S = S1 + S2 = 300 + 100 = 400 cm

Gráfica de la dependencia de la velocidad del cuerpo con el tiempo: foto

La distancia recorrida a diferentes velocidades se recorre en tiempos diferentes. Cuanto mayor sea la velocidad, menos tiempo se tarda en moverse.

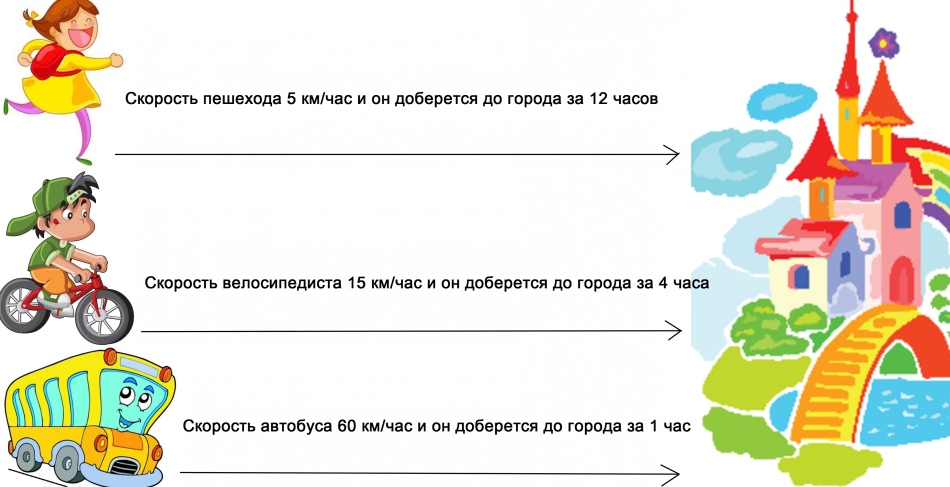
Tabla 4 clase: velocidad, tiempo, distancia

Nº	Velocidad (km/h)	Tiempo (hora)	Distancia (km)
1	5	2	?
2	12	?	12
3	60	4	?
4	?	3	300
5	220	?	440

Puedes fantasear y proponer tareas para el mesa usted mismo. A continuación se presentan nuestras opciones para las condiciones de las tareas:

1. Mamá le envió Caperucita Roja a la abuela. La niña se distraía constantemente y caminaba lentamente por el bosque, a una velocidad de 5 km/h. Pasó 2 horas en el camino. ¿Qué distancia caminó Caperucita Roja durante este tiempo?
2. El cartero Pechkin llevó un paquete en una bicicleta a una velocidad de 12 km/h. Sabe que la distancia entre su casa y la casa del tío Fedor es de 12 km. ¿Ayuda a Pechkin a calcular cuánto tardará en viajar?
3. Papá Ksyusha compró un auto y decidió llevar a la familia al mar. El automóvil viajaba a una velocidad de 60 km/h y se pasaron 4 horas en la carretera. ¿Cuál es la distancia entre la casa de Ksyusha y la costa del mar?
4. Los patos se juntaron en cuña y volaron hacia regiones cálidas. Las aves batieron sus alas incansablemente durante 3 horas y recorrieron 300 km durante este tiempo. ¿Cuál fue la velocidad de las aves?
5. El avión AN-2 vuela a una velocidad de 220 km/h. Despegó de Moscú y vuela a Nizhny Novgorod, la distancia entre estas dos ciudades es de 440 km.¿Cuánto tiempo estará el avión en el camino?

Las respuestas a los problemas dados se pueden encontrar en la siguiente tabla:

Nº	Velocidad (km/h)	Tiempo (hora)	Distancia (km)
1	5	2	10
2	12	1	12
3	60	4	240
4	100	3	300
5	220	2	440

Ejemplos de resolución de problemas de velocidad, tiempo y distancia para 4to grado

Si hay varios objetos en movimiento en una tarea, debe enseñarle al niño a considerar el movimiento de estos objetos por separado y solo luego juntos. Un ejemplo de tal tarea:

Dos amigos Vadyk y Tema decidieron salir a caminar y salieron de sus casas para encontrarse. Vadyk andaba en bicicleta y Tema caminaba. Vadyk conducía a una velocidad de 10 km/h y Tema caminaba a una velocidad de 5 km por hora. Una hora después se encontraron. ¿Cuál es la distancia entre las casas de Vadik y Tema?

Este problema se puede resolver usando la fórmula para la dependencia de la distancia en la velocidad y el tiempo.

S = v ⋅ t

La distancia recorrida por Vadyk en bicicleta será igual a su velocidad multiplicada por tiempo en tránsito.

S = 10 ⋅ 1 = 10 kilómetros

La distancia recorrida por el Sujeto se calcula de manera similar:

S = v ⋅ t

Sustituye los valores digitales de su velocidad y tiempo en la fórmula

S = 5 ⋅ 1 = 5 kilómetros

La distancia recorrida por Vadyk debe sumarse a la distancia recorrida por Tema.

10 + 5 = 15 kilómetros

¿Cómo aprender a resolver problemas complejos que requieren pensamiento lógico?

Para desarrollar el pensamiento lógico de un niño, es necesario resolver tareas lógicas simples y luego complejas a partir de ellos. Estas tareas pueden constar de varias etapas. Puede pasar de una etapa a otra solo si la anterior está resuelta. Un ejemplo de tal tarea:

Anton montó una bicicleta a una velocidad de 12 km/h, y Lisa montó un scooter a una velocidad 2 veces menor que la de Anton, y Denis caminó a una velocidad 2 veces menor que la de Lisa. ¿Cuál es la velocidad de Denis?

Para resolver este problema, primero debe conocer la velocidad de Lisa y luego la velocidad de Denis.

Dos ciclistas partieron de diferentes ciudades para encontrarse. Uno de ellos tenía prisa y corría a una velocidad de 12 km/h, y el segundo conducía tranquilamente a una velocidad de 8 km/h. La distancia entre las ciudades de donde partieron los ciclistas es de 60 km. ¿Qué distancia recorrerá cada ciclista antes de encontrarse? (solución debajo de la foto)

Solución:

• 12+8 = 20 (km/h) es la velocidad total de los dos ciclistas, o la velocidad a la que se acercaron
• 60: 20 = 3 (h) es el tiempo después del cual los ciclistas se encontraron
• 3 ⋅ 8 = 24 (km) es la distancia recorrida por el primer ciclista
• 12 ⋅ 3 = 36 (km) es la distancia recorrida por el segundo ciclista
• Comprueba: 36+24=60 (km) es la distancia recorrida por los dos ciclistas.
• Respuesta: 24 km, 36 km.

Ofrecer a los niños que resuelvan las siguientes tareas en forma de juego. Tal vez quieran hacer su propio problema sobre amigos, animales o pájaros.

VÍDEO: Problemas de movimiento