Área de un círculo: fórmula. ¿Por qué el área de un círculo descrito e inscrito en un cuadrado es igual a un triángulo isósceles de ángulo recto, un trapecio isósceles de ángulo recto?

¿Cómo encontrar el área de un círculo? Primero encuentra el radio. Aprende a resolver tareas simples y complejas.

Un círculo es una curva cerrada. Cualquier punto de la línea circular será equidistante del punto central. Un círculo es una forma plana, por lo que resolver la tarea de encontrar el área es simple. En este artículo, consideraremos cómo encontrar el área de un círculo inscrito en un triángulo, trapecio, cuadrado y descrito cerca de estas figuras.

Área de un círculo: fórmula usando radio, diámetro, longitud de un círculo, ejemplos de resolución de problemas

Para encontrar el área de ​​una figura, debes saber que tal es el radio, el diámetro y el número π.

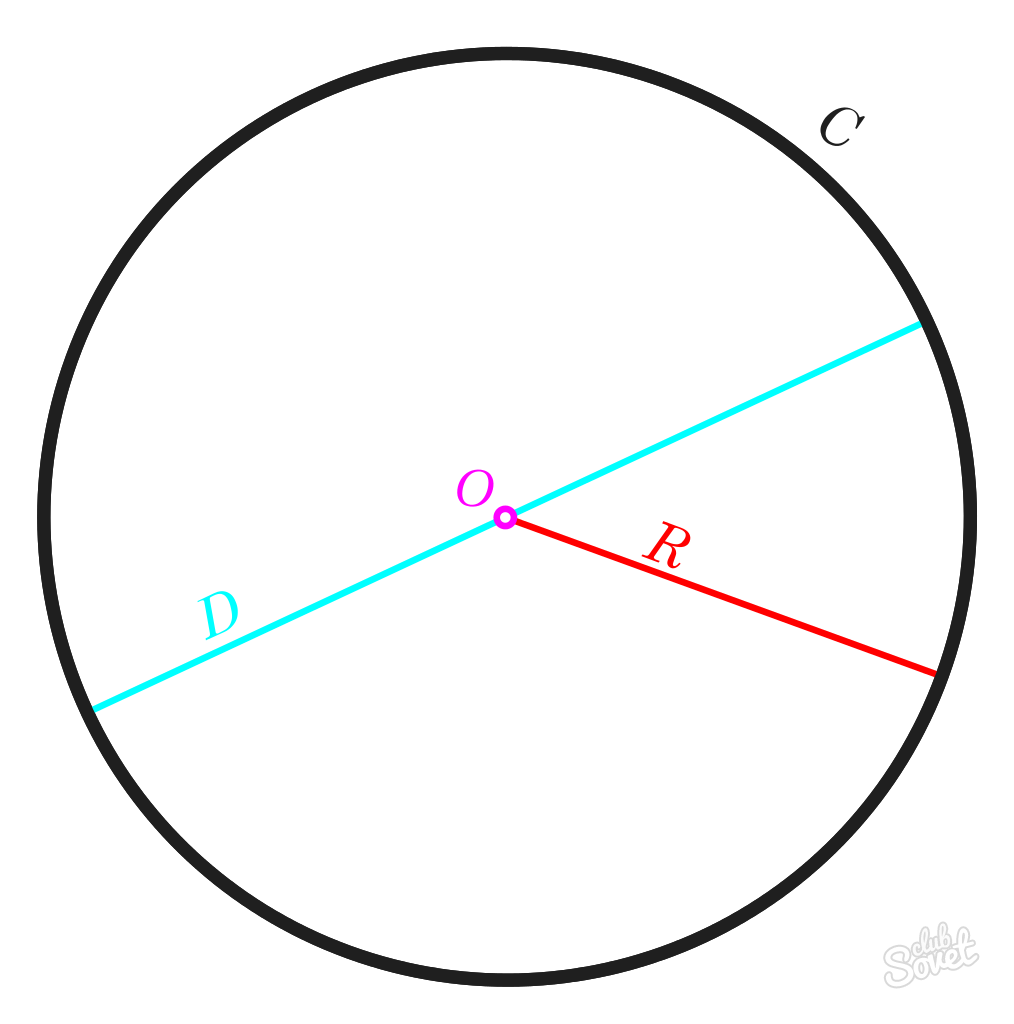
Radio R es la distancia delimitada por el centro del círculo. Las longitudes de todos los radios R de un círculo serán iguales.

El diámetro D es una línea entre dos puntos cualesquiera de un círculo que pasa por el punto central. La longitud de este segmento es igual a la longitud del radio R multiplicado por 2.

El número π es un valor constante igual a 3.1415926. En matemáticas, este número suele redondearse a 3,14.

La fórmula para encontrar el área de un círculo a través del radio:

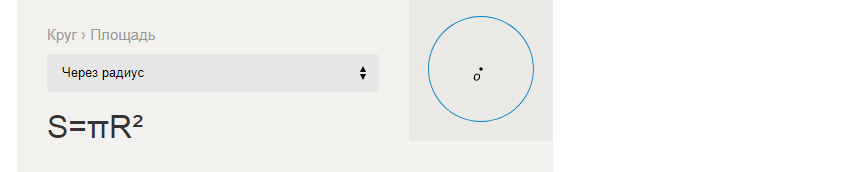
Ejemplos de tareas de resolución para encontrar el área S de un círculo a través del radio R:

---------- ---------------------------- --

Tarea: Encuentra el área de un círculo, si su radio es de 7 cm.

Solución: S=πR2, S=3,14*72, S=3,14*49=153,86 cm2.

Respuesta: El área de un círculo es 153,86 cm2.

La fórmula para encontrar el área S de un círculo a través del diámetro D:

Ejemplos de tareas de resolución para encontrar S si se conoce D:

--------- --------------------------------

Búsqueda: Encuentra S de un círculo, si su D es igual a 10 cm.

Solución: P=π*d2/4, P=3,14*102/4=3,14*100/4=314/4=78,5 cm2.

Respuesta: El área de una figura redonda plana es de 78,5 cm2.

Encontrar S de un círculo, si se conoce la longitud del círculo:

Primero, encontramos cuál es el radio. La longitud del círculo se calcula mediante la fórmula: L=2πR, en consecuencia, el radio R será igual a L/2π. Ahora encontramos el área del círculo usando la fórmula a través de R.

Consideremos la solución en el ejemplo del problema:

) ----------- --------------------------------------------

Tarea: Encuentra el área de un círculo, si se conoce la longitud del círculo L — 12 cm.

Solución: Primero encontramos el radio: R=L/2π=12/2*3.14=12/6.28=1.91.

Ahora encontramos el área a través del radio: S=πR2=3.14*1.912=3.14*3.65=11.46 cm2.

Respuesta: El área de un círculo es 11,46 cm2.

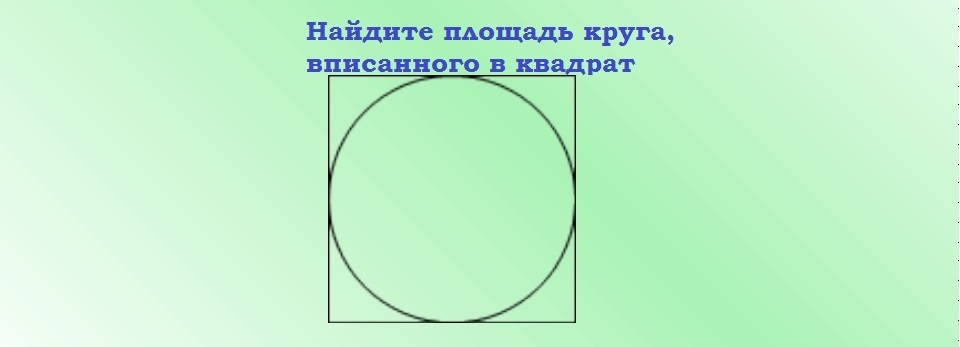
Área de un círculo inscrito en un cuadrado: fórmula, ejemplos de resolución de problemas

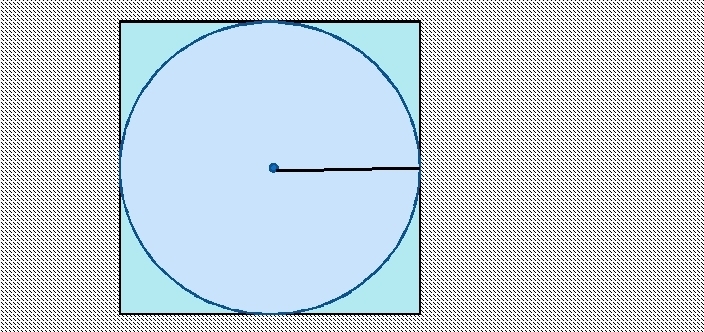
Encontrar el área de un círculo inscrito en un cuadrado es simple. El lado del cuadrado es el diámetro del círculo. Para encontrar el radio, necesitas dividir el lado por 2.

La fórmula para encontrar el área de un círculo inscrito en un cuadrado:

Ejemplos de resolución de problemas para hallar el área de un círculo inscrito en un cuadrado:

-- --------------------------------- ----

Tarea No. 1: Se conoce el lado de una figura cuadrada, que mide 6 centímetros. Encuentre el área S del círculo inscrito.

Solución: S=π(a/2)2=3,14(6/2)2=3,14*9=28,26 cm2.

Respuesta: El área de una figura redonda plana es 28,26 cm2.

----------------------------------------- -----------

Tarea #2 :Encuentra S de un círculo inscrito en una figura cuadrada y su radio si un lado es igual a a=4 ver

Resolver de la siguiente manera : Primero encontramos R=a/2=4/2=2 ver

Ahora hallaremos el área del círculo S=3.14*22=3.14*4=12.56 cm2.

Respuesta: El área de una figura circular plana es 12,56 cm2.

Área de un círculo circunscrito a un cuadrado: fórmula, ejemplos de resolución de problemas

Es un poco más difícil encontrar el área de una figura redonda descrita alrededor de un cuadrado. Pero, conociendo la fórmula, puede calcular rápidamente este valor.

Fórmula para hallar S de un círculo circunscrito a una figura cuadrada:

Ejemplos de resolución de problemas para encontrar el área de un círculo descrito alrededor de una figura cuadrada:

Problema

Área de un círculo inscrito en un triángulo rectángulo e isósceles: fórmula, ejemplos de resolución de problemas

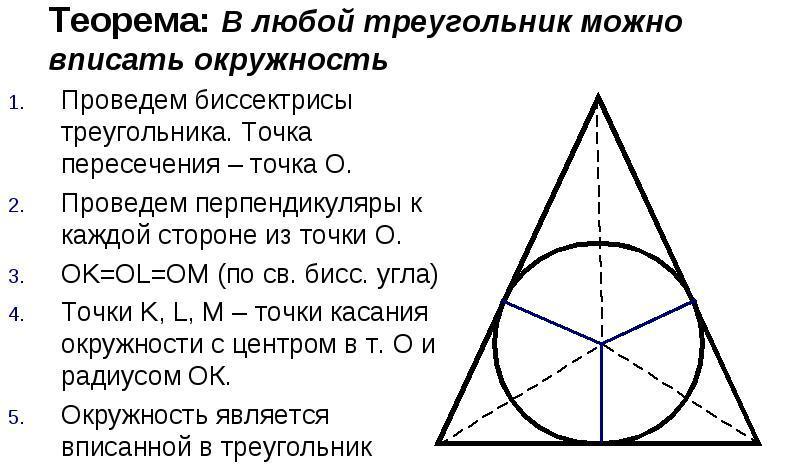
Un círculo inscrito en una figura triangular es un círculo que toca los tres lados del triángulo. Cualquier figura triangular se puede inscribir con un círculo, pero solo uno. El centro de la circunferencia será el punto de intersección de las bisectrices de los ángulos del triángulo.

Fórmula para encontrar el área de un círculo inscrito en un triángulo isósceles:

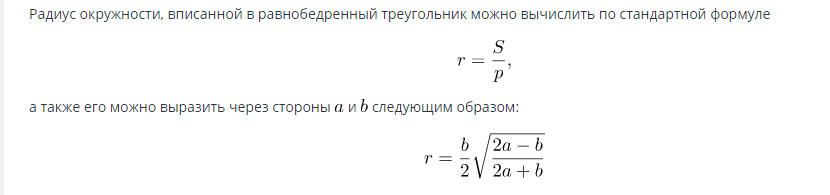
Cuando se conoce el radio, el área se puede calcular mediante la fórmula: S=πR2.

Fórmula para encontrar el área de un círculo inscrito en un triángulo rectángulo:

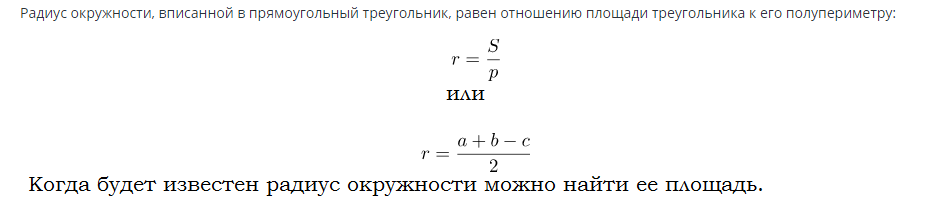
Ejemplos de solución de problemas:

Problema # 1

)

Si en este problema también necesitas encontrar el área de un círculo con un radio de 4 cm, entonces puedes hacerlo mediante la fórmula: S=πR2

Tarea #2

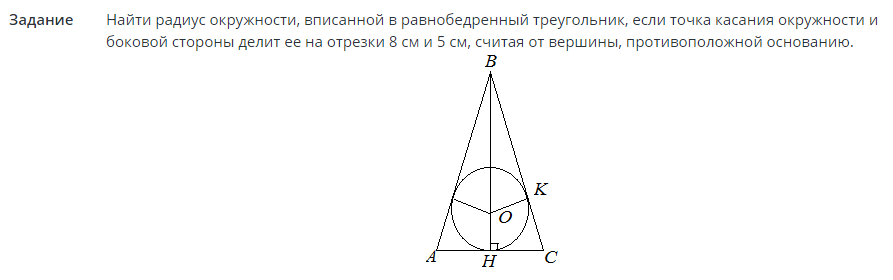
Soluciones:

Ahora que se conoce el radio, el área del círculo se puede encontrar en términos del radio. Consulte la fórmula anterior en el texto.

Tarea #3

Área de un círculo circunscrito a un triángulo rectángulo e isósceles: fórmula, ejemplos de resolución de problemas

Todas las fórmulas para encontrar el área de un círculo se reduce al hecho de que primero necesitas encontrar su radio. Cuando se conoce el radio, encontrar el área es simple, como se describió anteriormente.

​​

El área de un círculo circunscrito a un triángulo rectángulo e isósceles se encuentra mediante la siguiente fórmula:

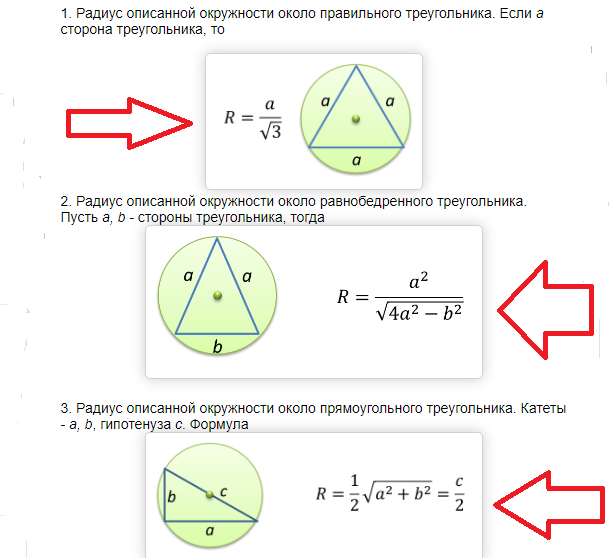
Ejemplos de resolución de problemas:

Aquí hay otro ejemplo de resolución de un problema utilizando la fórmula de Heron.

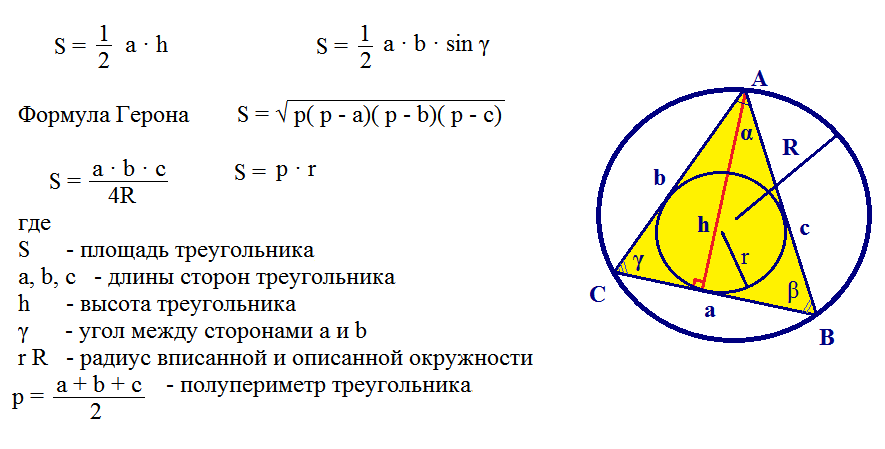
Es difícil de resolver problemas similares, pero se pueden superar si conoce todas las fórmulas. Los estudiantes resuelven tales tareas en el noveno grado.

Área de un círculo inscrito en un trapezoide rectangular e isósceles: fórmula, ejemplos de resolución de problemas

Por ejemplo, un trapezoide isósceles está inscrito con un círculo que está en el punto de contacto divide un lado en segmentos m y n.

Para resolver este problema, es necesario utilizar las siguientes fórmulas:

Encontrar el área de un círculo inscrito en un trapezoide rectangular se realiza de acuerdo con la siguiente fórmula:

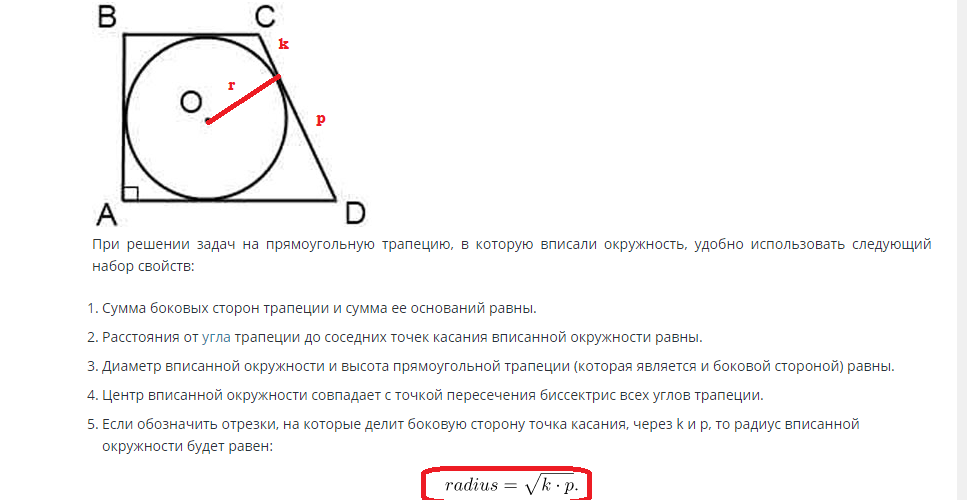
Si se conoce el lado, entonces el radio se puede encontrar a través de este valor. La altura del lado del trapezoide es igual al diámetro del círculo, y el radio es la mitad del diámetro. En consecuencia, el radio es igual a R=d/2.

Ejemplos de resolución de problemas:

Área de un círculo circunscrito a un trapezoide rectángulo e isósceles: fórmula, ejemplos de resolución de problemas

Se puede inscribir un trapezoide en un círculo cuando la suma de los ángulos opuestos es 180°. Por lo tanto, solo se puede inscribir un trapezoide equilátero. El radio para calcular el área de un círculo descrito cerca de un trapezoide rectangular o isósceles se calcula mediante las siguientes fórmulas:

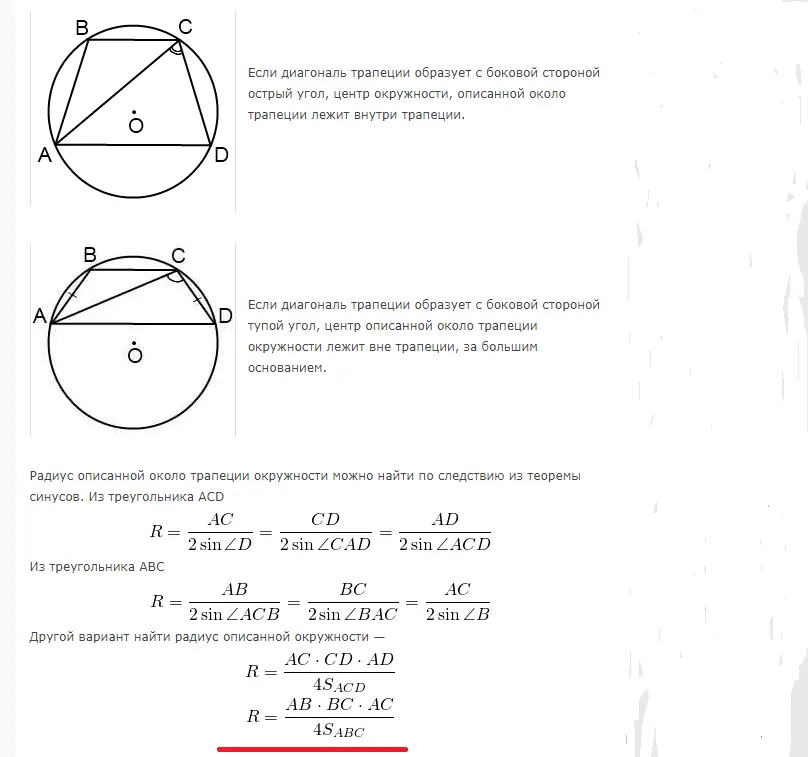
Ejemplos de resolución de problemas:

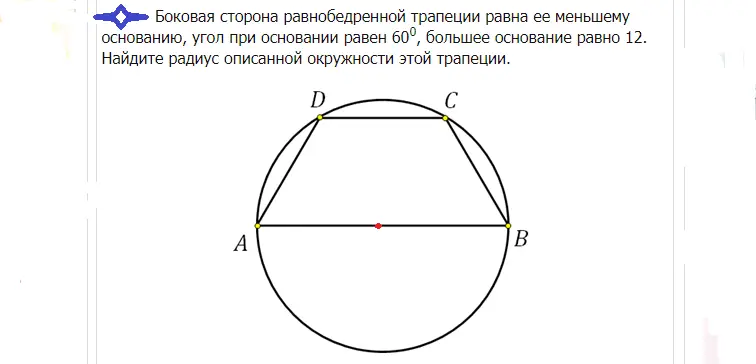
Solución: La base grande en este caso pasa por el centro, ya que un trapezoide isósceles está inscrito en el círculo. El centro divide esta base exactamente por la mitad. Si la base AB es igual a 12, entonces el radio R se puede encontrar de la siguiente manera: R=12/2=6.

Respuesta: El radio es 6.

En geometría, es importante saber fórmulas. Pero es imposible recordarlos todos, por lo que incluso en muchos exámenes se permite usar un formulario especial. Sin embargo, es importante poder encontrar la fórmula correcta para resolver este o aquel problema. Practique resolver varios problemas para encontrar el radio y el área de un círculo para poder sustituir fórmulas correctamente y obtener respuestas precisas.

Vídeo: Matemáticas | Cálculo de las áreas de un círculo y sus partes